The Earth’s magnetic field may approximate to a simple dipole, but explaining precisely how that dipole is generated and maintained is not simple at all. The field originates deep in the Earth, where temperatures are far too high for any material to maintain a permanent magnetisation; the dynamism that is apparent from the wandering of the magnetic poles with respect to the spin axis (secular variation), and the quasi-periodic flips in field polarity, also suggest that some process is actively generating and maintaining the geomagnetic field. Geophysicists therefore look to the most dynamic region in the planetary depths, the molten outer core, as the source of the force that directs our compass needles.
One of the more important processes going on in the core is the slow growth of the solid inner core at the expense of the outer core, as the centre of the Earth loses heat to the mantle, and ultimately the surface. As the iron crystallises, it releases latent heat, generating thermal buoyancy forces. Additionally, seismic measurements show that whilst the outer core is much less dense than experiments and calculations predict, this deficit is much smaller in the inner core; therefore crystallisation also leaves behind the lighter elements that make up around 10% of the outer core (it’s not entirely certain what these elements are, but sulphur is a popular candidate), generating strong compositional buoyancy forces. Together with a possible contribution from heat generated by radioactive decay, these buoyancy forces drive vigorous convection of the outer core, with flow rates of the order of 10 kilometres per year.
As you may dimly remember from school, the motion of a conductor in a magnetic field generates a current; currents also generate their own magnetic field. The iron in the outer core is a conductor, so its motion in the presence of the existing geomagnetic field induces electric currents, generating new magnetic flux, as well as forces that modify the pattern of convective flow. The key to a stable, self-sustaining geodynamo is that these processes feed back on each other, until the pattern of induced currents – both electrical and convective – generates a magnetic field that has the same, or almost the same, configuration as the input field, reinforcing and maintaining it over geological time. The field induces currents which generate the field. This is no free lunch: Ohm’s law dictates that resistance to the electrical current flow will cause energy to be lost from the system, so without the external input of energy from convection, within a thousand years or so the field would weaken and die.
You can get your head round this idea without developing too much of a headache, even if the ‘geodynamo’ looks nothing like any electrical generator that humans have ever imagined. However, matching this general account to the actual behaviour of the actual magnetic field of the Earth, in all its polar wandering, polarity reversing, glory – is not so easy, not least because many of the physical parameters that control convective flow, such as the viscosity of the outer core, are poorly constrained. Plus, magnetohydrodynamic modelling is as fiendishly complicated as its name suggests. So it was quite a surprise when in almost the first serious attempt, Glatzmaier and Roberts [1] managed to produce a model that not only produced a self-sustaining dipole field that looked a lot like the Earth’s, but also went through periodic spontaneous reversals (click the link to see some animations).
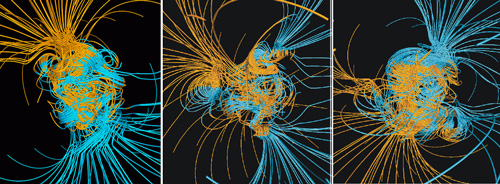
This behaviour was rather unexpected, because the set-up of the model was governed by what was computationally feasible, meaning that it wasn’t particularly focussed on trying to match the real conditions in the Earth’s core (Glaztmaier and Roberts were aiming more at establishing the validity of the proposed dynamo mechanism in general). But it turned out that they had got one important boundary condition right: the Earth’s rotation, which has a strong influence on the patterns of convection in the outer core. Most significantly, it has a tendency to produce helical convection currents which align with the spin axis (the strong orange lines in the figure below show the spiralling motion that the rotation of the core superimposes on the larger-scale currents, represented by the thicker, fainter lines). This helical flow tangles up the magnetic flux within the core; flux lines (blue) only tend to escape the core at higher latitudes where the helical flows intersect with the core-mantle boundary, giving the field its overall dipolar shape.
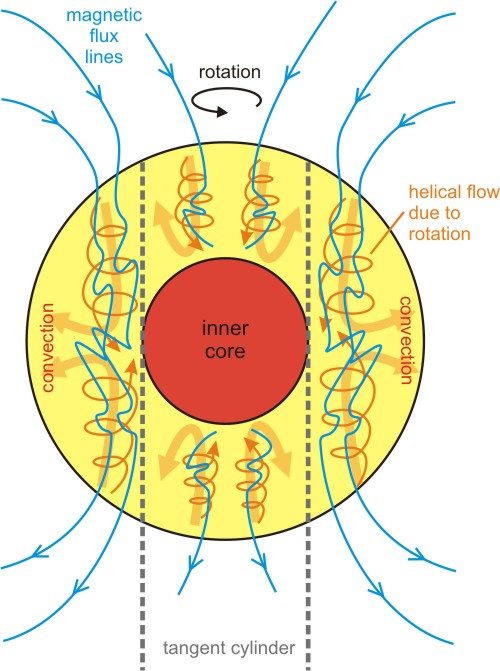
Thus, it seems that to a first approximation, any spinning, convecting, conductive shell will tend to produce a magnetic field which broadly looks like the Earth’s. Some caution is still required, though; if you remember, the Earth’s field also looks like a bar magnet, so we already know that very different mechanisms can produce similar looking magnetic results. Thus, it’s still hard to say for sure how well this picture actually represents what’s going on in the Earth’s outer core; but this sort of model does give us a useful starting point to direct our studies. For example, these models suggest that one useful place to focus on might be at high latitudes, within the zone where the ‘tangent cylinder’ of the inner core intersects with the surface. If our models are correct, within the tangent cylinder the inner core acts as an impediment to convective flow, reducing the length scale of the circulating currents and increasing the overall variability of the local field. This is something that we can go and look for. Additionally, by comparing the geological record of field behaviour – the rate and character of reversals and secular variation over time – to the behaviour of different models run with different physical properties, we might be able to better constrain parameters like the viscosity and composition of the outer core. And once we properly understand the origin and behaviour of today’s magnetic field, we might have some idea of what is was like in the distant past. Is it reasonable to assume that the field has always been dipolar? That’s certainly a question I’d like to answer – although I think I’ll leave the 4th order differential equations to somebody else.
[1] G.A. Glatzmaier and P.H. Roberts, “A three-dimensional self-consistent computer simulation of a geomagnetic field reversal,” Nature, 377, 203-209 (1995).



Comments (9)